mamoc

Agent-Based BTC Trading in a Limit Order Book

Alex Cheetham

Recreating the DBBA agent-based BTC-GBP market model with chartists, noise traders, and a limit order book that reproduces key stylised facts.

Alex CheethamAlex CheethamAlex CheethamAlex Cheetham
Cover image for Agent-Based BTC Trading in a Limit Order Book

Project overview

This article covers the design of an agent-based Bitcoin market (BTC/GBP) inside a limit order book (LOB) and test whether it reproduces core stylised facts — heavy-tailed returns, volatility clustering, and a unit-root price process. The market mixes rule-based chartists with noise traders, extends Cocco et al.’s specification (Cocco et al., 2019), and benchmarks the output against real BTC data.

Agent architecture

All agents inherit from an abstract base class that holds cash and crypto balances, a handle to the market, and helpers for opening or closing positions.

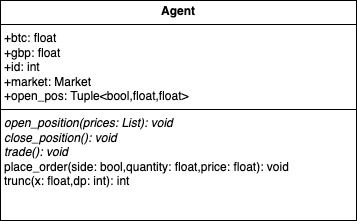
Abstract agent UML diagram. Italic labels denote abstract methods.
Figure 1:
Abstract agent UML diagram. Italic labels denote abstract methods.

Chartists

Chartists follow technical rules driven by either momentum or RSI signals, mirroring the setup analysed by Cocco, Tonelli, and Marchesi. Four subtypes alter the weighting between the rules:

SubtypeWeighting
HighMom0.8
HighRSI0.2
Balanced0.5
Alternating"alt"

For non-alternating subtypes, a uniform random draw chooses the strategy:

x∼U(0,1),Strategy={Momentumx<self.weightingRSIx≥self.weightingx \sim \mathcal{U}(0, 1), \qquad \text{Strategy} = \begin{cases} \text{Momentum} & x < \texttt{self.weighting} \\ \text{RSI} & x \ge \texttt{self.weighting} \end{cases}

Alternating chartists inspect the weekly volatility of the last 30 prices:

def weekly_volatility(self, prices, threshold=0.025):
    if len(prices) < 30:
        return False
    recent_daily_returns = pd.DataFrame(prices[-30:])
    daily_std_dev = recent_daily_returns.pct_change(1).std()[0]
    weekly_volatility = daily_std_dev * np.sqrt(7)
    return weekly_volatility > threshold

An excerpt of the order placement logic highlights how RSI and momentum signals translate into limit orders:

if self.open_pos is None and mom:
    action = 1  # Buy
    delta = (prices[-1] - prices[0]) / len(prices)
    period = random.randint(1, len(prices) // 2)
    price = prices[-1] + 0.9 * (delta * period)
    quantity = self.risk * curr[action] / price
    self.place_order(action, trunc(quantity), price)
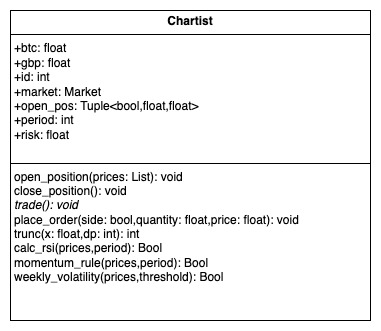
Chartist UML structure showing the shared base class and subtype behaviour.
Figure 2:
Chartist UML structure showing the shared base class and subtype behaviour.

Noise traders

Noise traders inject stochastic liquidity, capturing the volatility effects highlighted in recent agent-based market studies (Dai et al., 2023). At each step they either open or close a position at a randomly sampled price:

Ptarget∼N(Pt,σ),Qtrade∼U ⁣(0.1⋅holdings, holdings)P_\text{target} \sim \mathcal{N}(P_t, \sigma), \qquad Q_\text{trade} \sim \mathcal{U}\!\left(0.1 \cdot \text{holdings},\, \text{holdings}\right)

The expected transaction amount is therefore

E[Transaction]=E[Qtrade]⋅E[Ptarget]=0.55⋅holdings⋅Pt/2,\mathbb{E}[\text{Transaction}] = \mathbb{E}[Q_\text{trade}] \cdot \mathbb{E}[P_\text{target}] = 0.55 \cdot \text{holdings} \cdot P_t / 2,

producing net-neutral pressure in expectation while amplifying return variance.

AspectRandom TradersChartists
Decision processUniform random choicesTechnical indicators (RSI, momentum)
MotivationLiquidity/noiseProfit-seeking
Price targetingNormal around current priceDirectional based on indicator
Market impactAdds noise, occasionally dampens trendsReinforces prevailing trends
Risk managementNoneAgent-specific appetite (self.risk)

Market design

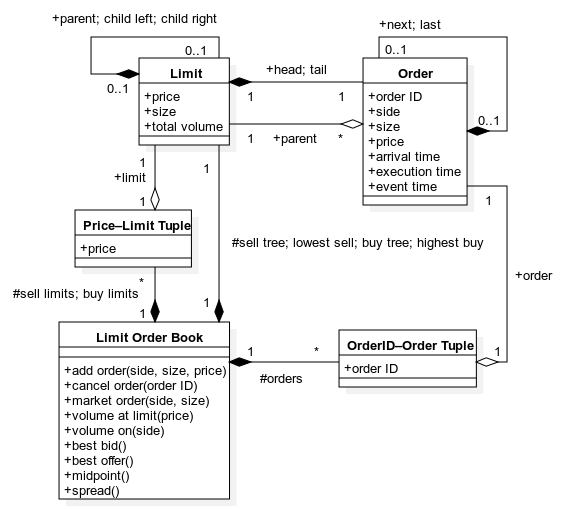
Kautenja's price-time priority limit order book used as the market core.
Figure 3:
Kautenja's price-time priority limit order book used as the market core.

The market wraps Kautenja’s LOB implementation, enabling partial order fills and price-time matching. Three key adaptations were required to satisfy cryptocurrency constraints:

  1. Fractional Bitcoin: Orders can trade BTC to 5 decimal places, matching exchange minimums (e.g., Kraken Support).
  2. Position flexibility: Agents may submit any sequence of buys and sells subject to available balances—no enforced “flat” state.
  3. Fractional price response: The price impact function drops the floor operator so the tick size is continuous (Petrov, 2019). r_n(ΔN_n) = α · sgn(ΔN_n) · √(|ΔN_n|).
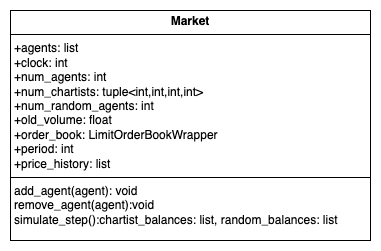
Market class UML diagram showing interactions between agents and the LOB.
Figure 4:
Market class UML diagram showing interactions between agents and the LOB.

The simulate_step routine shuffles agents each turn, lets them trade, applies the price impact rule, and appends the updated price to history. Wealth injections of 10% emulate capital inflows observed in crypto markets and help trigger momentum. Baseline supply, address counts, and price levels follow January 1st 2020 observations of the BTC network (BitInfoCharts; Blockchain.com; Yahoo Finance).

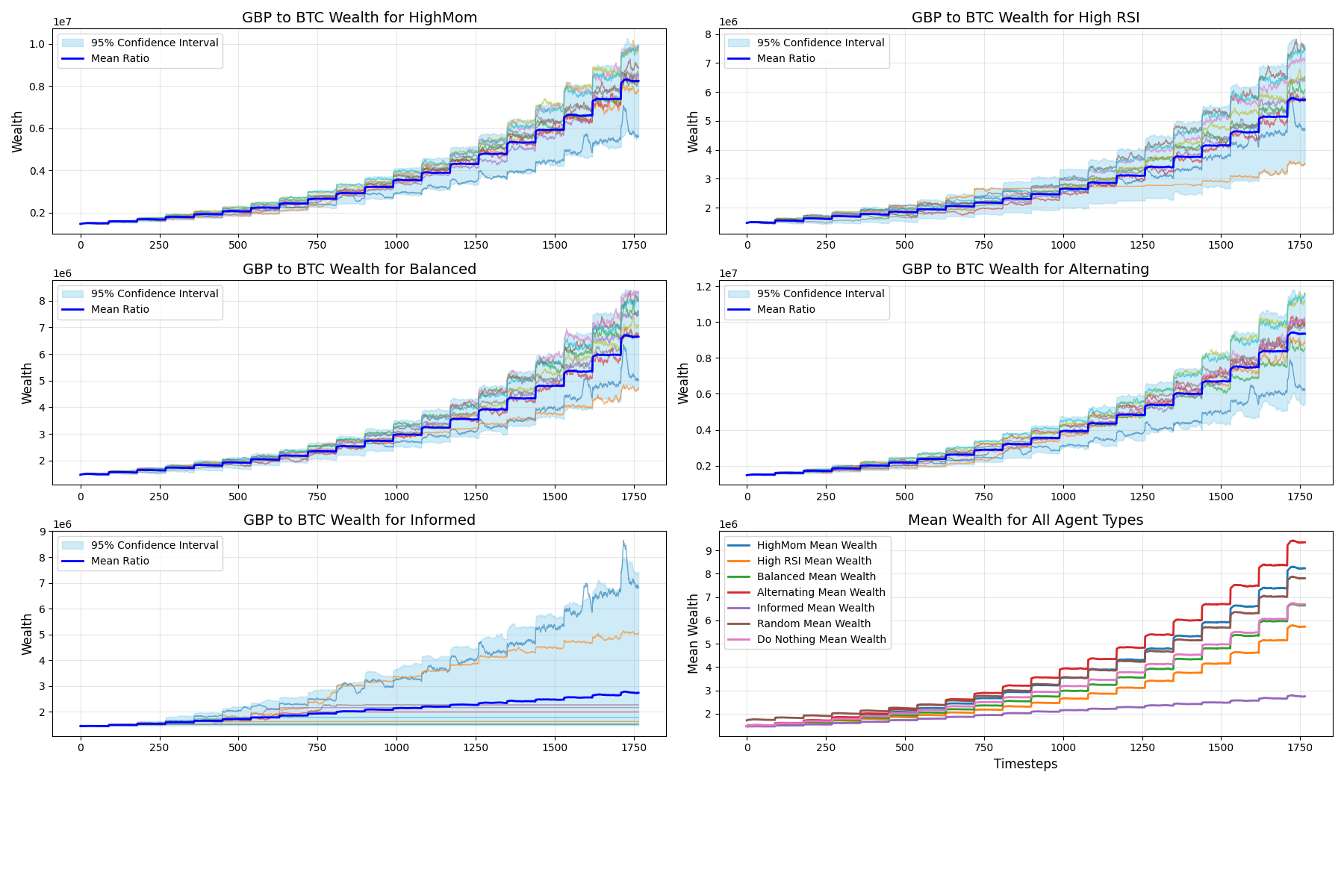
Stylised facts reproduced

The model replicates Cocco et al.’s findings that, in a chartist/noise-trader ecosystem, returns remain heavy-tailed and volatility clusters even without fundamental value traders (Cocco et al., 2019).

Distribution of absolute returns, squared returns, and autocorrelation for the baseline simulation.
Figure 5:
Distribution of absolute returns, squared returns, and autocorrelation for the baseline simulation.
Autocorrelation of absolute returns shows slow decay consistent with volatility clustering.
Figure 6:
Autocorrelation of absolute returns shows slow decay consistent with volatility clustering.

Activating informed momentum (RSI + alternating chartists) and periodic wealth injections magnifies these effects without breaking plausibility.

Metric distribution after enabling informed momentum traders, highlighting fatter tails.
Figure 7:
Metric distribution after enabling informed momentum traders, highlighting fatter tails.
Wealth evolution when traders receive 10% injections, producing bursts of momentum-driven activity.
Figure 8:
Wealth evolution when traders receive 10% injections, producing bursts of momentum-driven activity.

Momentum lookback windows ( n \in [1, 30] ) balance the Efficient Market Hypothesis—which argues that historical prices offer little predictive power (Fama, 1970)—with empirical evidence of short-lived inefficiencies in equity and cryptocurrency markets (Jiang, 2011; Al-Yahyaee et al., 2020). The shorter horizons allow chartists to exploit transient order-imbalance and liquidity effects without contradicting longer-run market efficiency.

Comparison with Cocco et al.

Price trajectories, volume, and mean reversion were benchmarked against Section 3 of the reference model (Cocco et al., 2019).

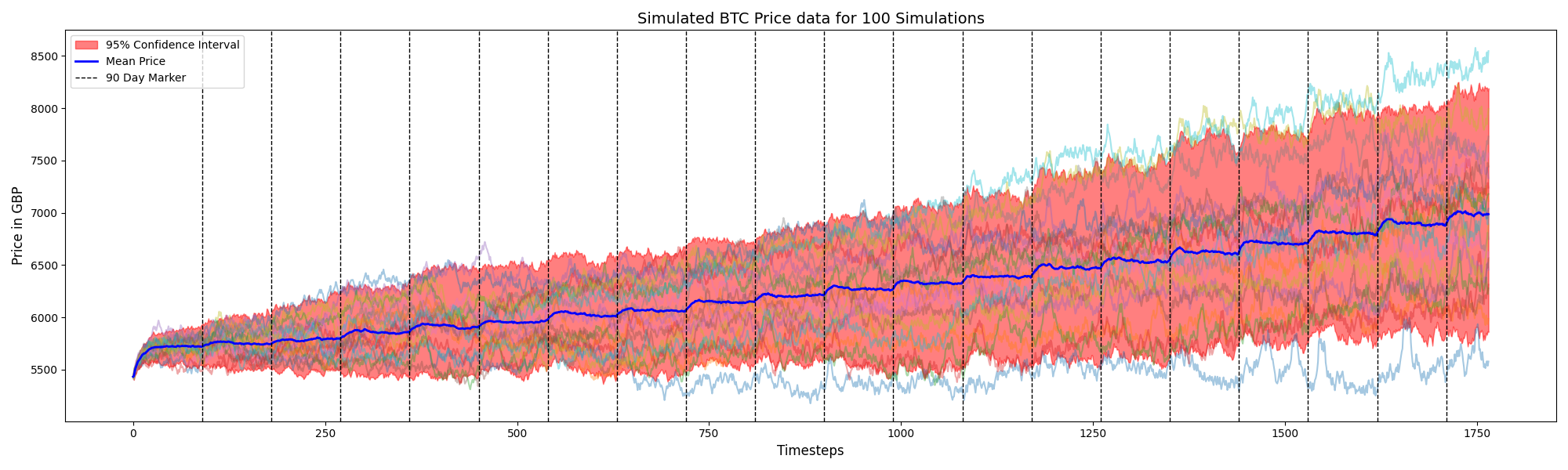
Simulated BTC-GBP price path showing momentum bursts aligned with wealth injections.
Figure 9:
Simulated BTC-GBP price path showing momentum bursts aligned with wealth injections.
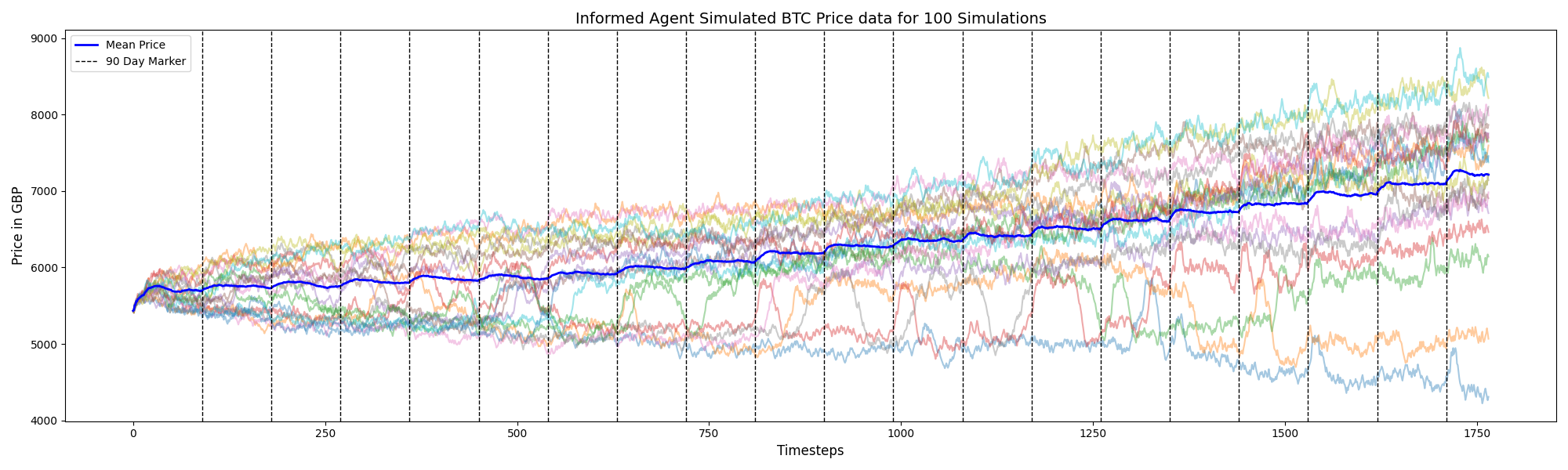
Price path once informed chartists are activated; richer dynamics but still mean-reverting around the unit root.
Figure 10:
Price path once informed chartists are activated; richer dynamics but still mean-reverting around the unit root.
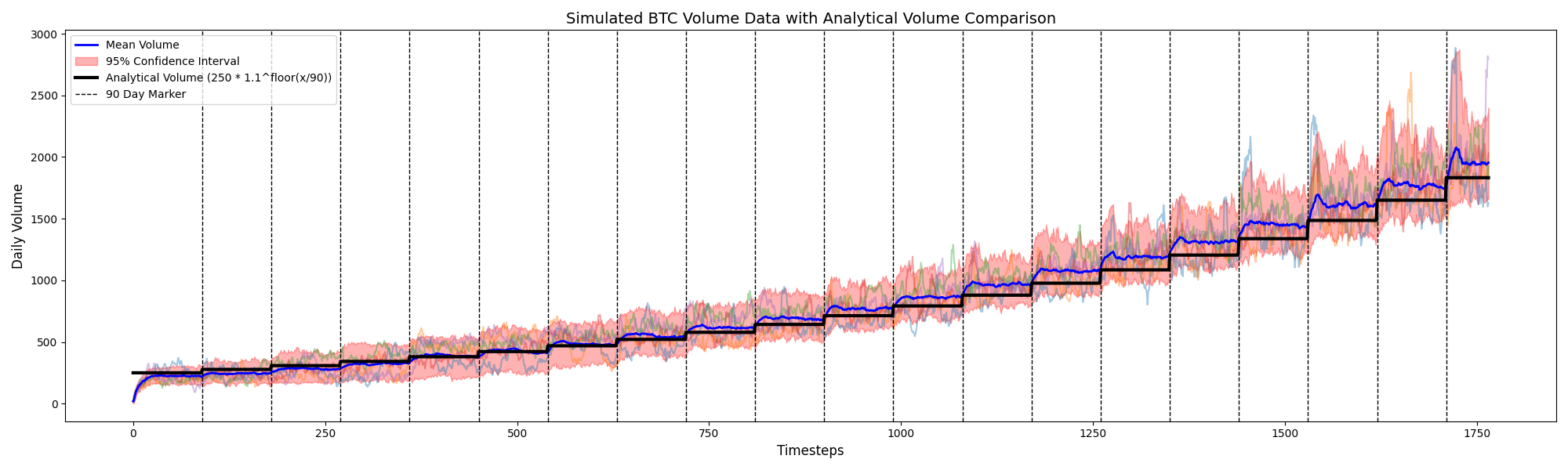
Daily traded volume across 100 simulations; the upward drift reflects broader participation after each wealth injection.
Figure 11:
Daily traded volume across 100 simulations; the upward drift reflects broader participation after each wealth injection.
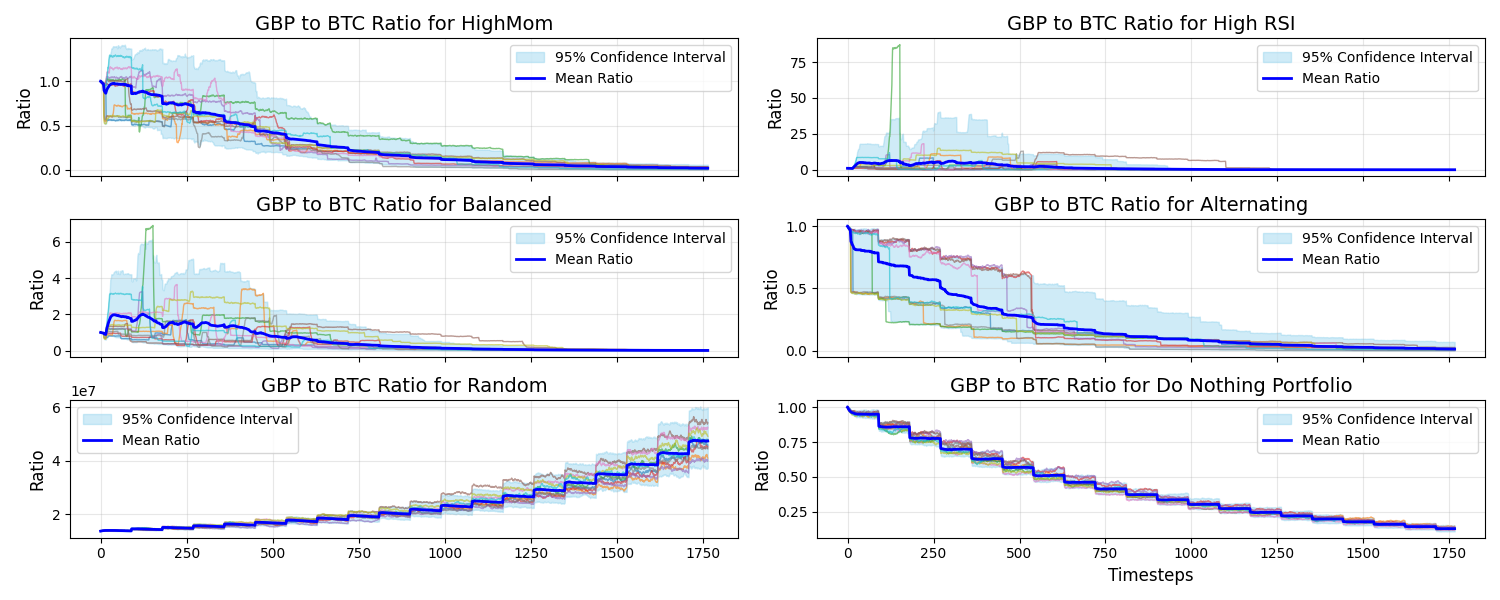
Bid-ask imbalance ratio compared with the reference model.
Figure 12:
Bid-ask imbalance ratio compared with the reference model.

Both frameworks deliver upward-trending prices, but wealth injections induce more realistic surges in this implementation. Volumes also scale closer to observed BTC markets once rescaled by 1,000, because liquidity is not confined to a single cohort of agents.

Validation with real BTC data

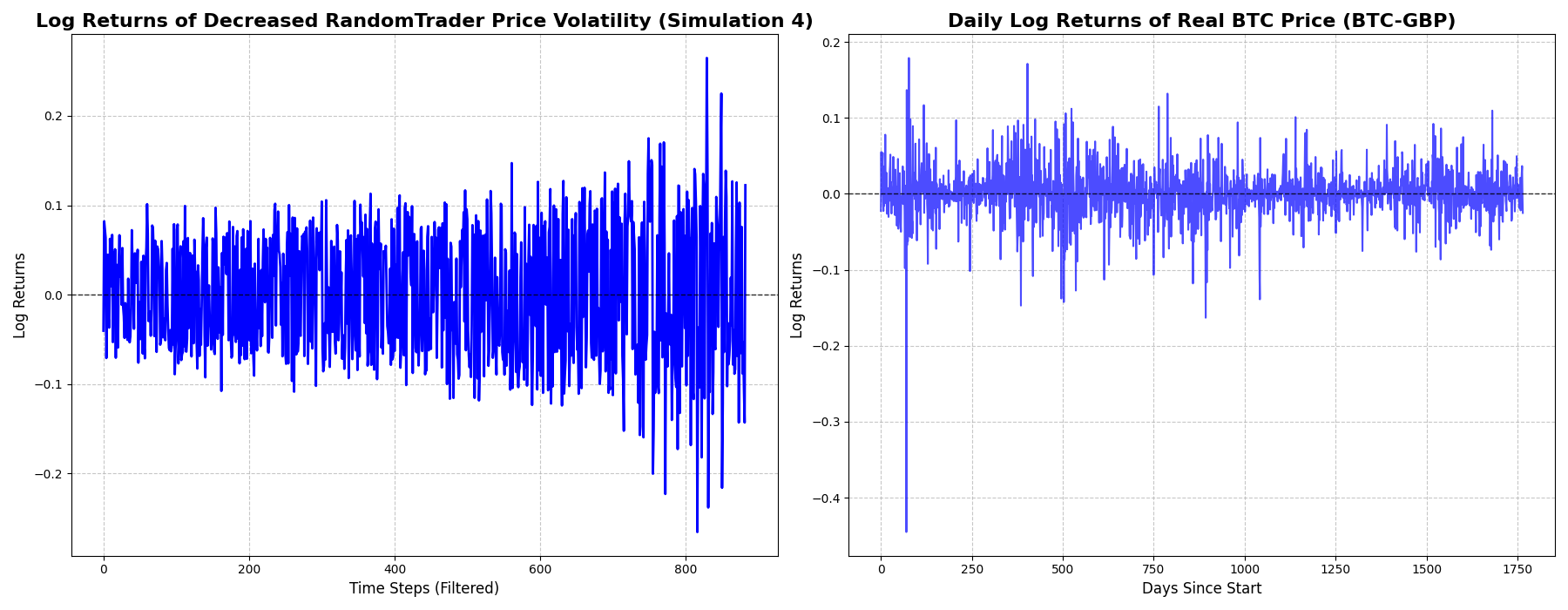
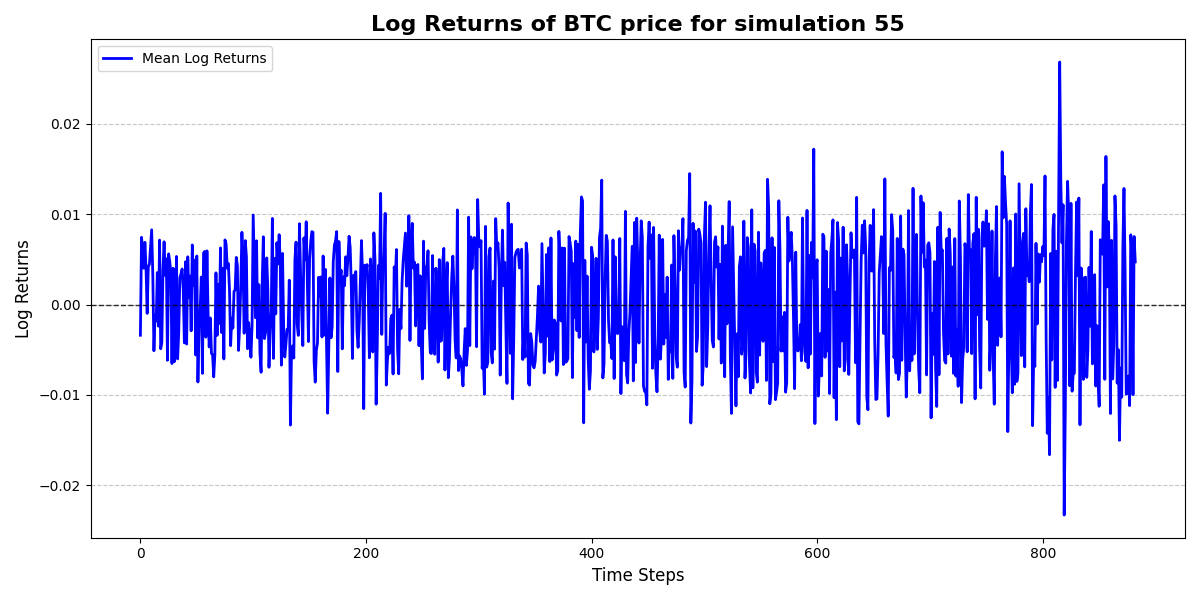
Log-return distributions match actual BTC-GBP series (2018–2024) and retain volatility spikes between 0.1 and 0.3.

Log returns for real BTC-GBP data.
Figure 13:
Log returns for real BTC-GBP data.
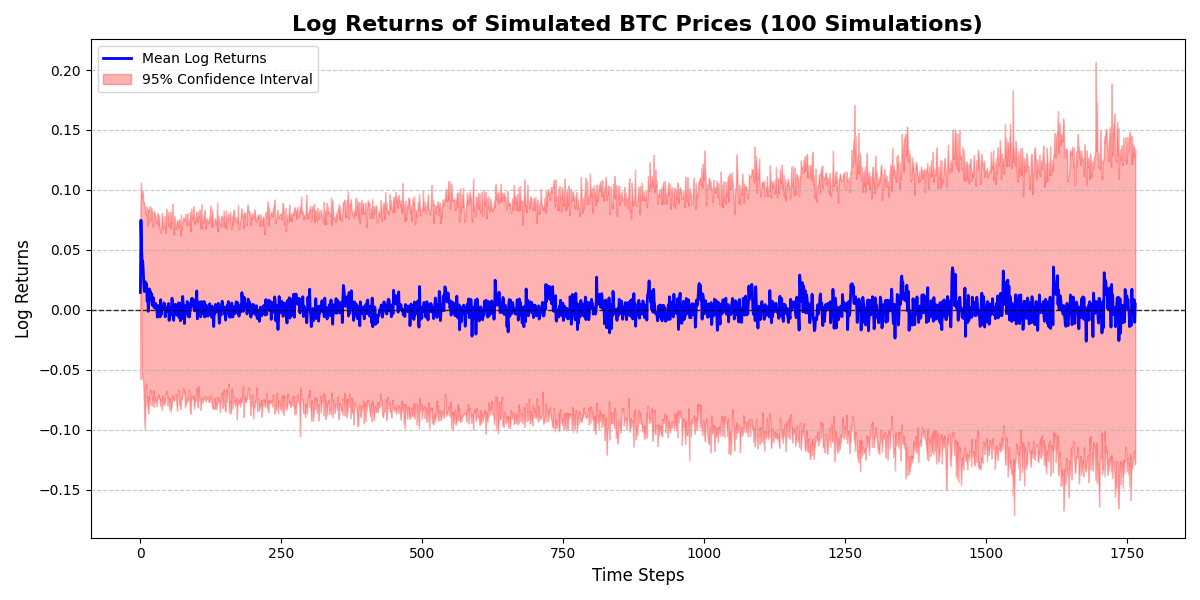
Log returns for the simulated market; note the similar volatility bursts.
Figure 14:
Log returns for the simulated market; note the similar volatility bursts.

Unit-root behaviour holds under the Augmented Dickey-Fuller test:

DatasetTest statisticp-value
Real prices-1.02300.7448
Log real prices-1.60280.4822
Simulated price (mean)-1.32370.6213

Additional stylised stats:

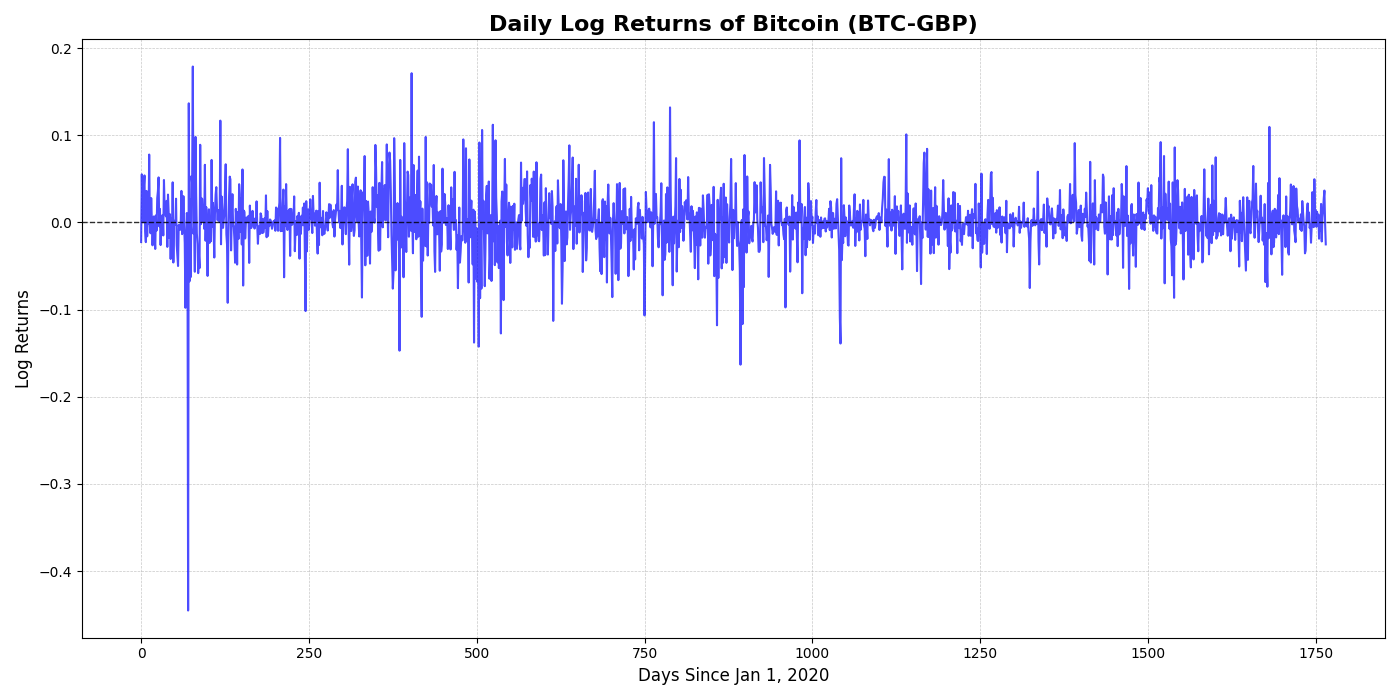
Rolling statistics for real BTC log returns.
Figure 15:
Rolling statistics for real BTC log returns.
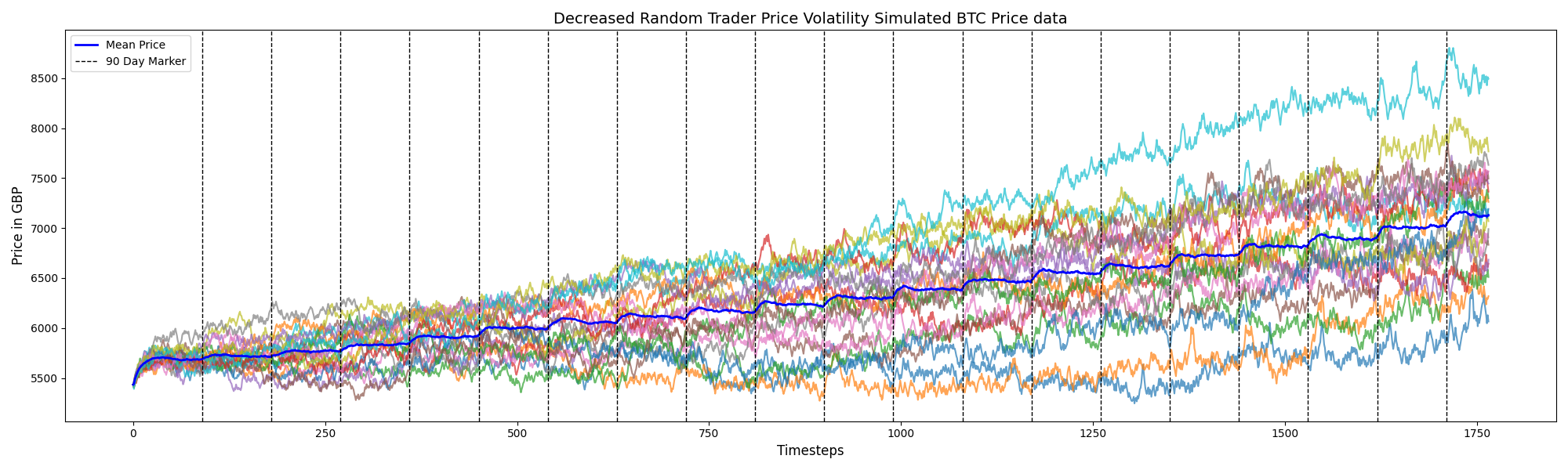
Volatility clustering under reduced momentum parameters.
Figure 16:
Volatility clustering under reduced momentum parameters.
Alternative volatility scenario with damped wealth injections.
Figure 17:
Alternative volatility scenario with damped wealth injections.
Distribution of RSI and momentum-triggered trades across subtypes.
Figure 18:
Distribution of RSI and momentum-triggered trades across subtypes.
Example single-run trajectory showing alternating RSI and momentum dominance.
Figure 19:
Example single-run trajectory showing alternating RSI and momentum dominance.

Takeaways for DBBA Capital

  • Momentum plus noise recreates Bitcoin’s signature pathologies. The LOB model delivers fat tails, clustered volatility, and a price process that fails to reject a unit-root null (Cocco et al., 2019).
  • Wealth injections act as policy levers. Capital inflows trigger realistic breakouts; withdrawing them returns to a calmer regime.
  • Noise traders are essential. They add liquidity, occasionally offset chartist herding, and supply the randomness needed for fat-tailed returns (Dai et al., 2023; Kauffman et al., 2023). Choi et al. highlight how individual traders can distort valuations even in regulated markets (Finance Research Letters).
  • Model ready for extensions. Adding transaction costs, fundamentalists, or exchange microstructure quirks would be the next steps to increase realism further (Cocco et al., 2017).
← Back to home
placeholder